Learning basic TensorFlow, Keras by examples of CNN implementation! - Part I
In this tutorial, we learn TensorFlow, Keras by going step by step from simple thing to recent state-of-the-art neural network in computer vision. At the beginning of the tutorial, we learn how to implement Convolutional Neural Networks (CNN) by TensorFlow and more efficient tool Keras. Towards the end of this tutorial, you can go advance to implement from the scratch state-of-the-art CNN, such as: VGG, Inception V4, DenseNet, etc. If you are not familiar with CNN, I recommend to take a look this tutorial first: http://cs231n.github.io/convolutional-networks/
What is TensorFlow (TF) and Keras?
Keras is a high-level Python API, which is designed to quickly build and train neural networks using either TensorFlow or Theano. It is developed by François Chollet.
Why TF and Keras?
Keras is hailed to be the future of deep learning framework.
Installing Keras on TensorFlow
Learning Keras by examples
Let’s start Keras excervise by the simple classification problem by using linear regression and softmax, which is often considered as the hello world lesson in machine learning.
Example 1: MNIST classification by logistic regression
MNIST dataset
TensorFlow implementation
Data preparation: Tensorflow provide function that we can easily download and prepare MNIST data by one line of Python code. To facilitate for our learning and implementation in the next lesson, we put the code in a single file: e.g. datatool/datasets.py.
from tensorflow.examples.tutorials.mnist import input_data
def read_tf_mnist(data_dir):
# Read MNIST data by TensorFlow
# mnist.train.images [N 784]
# mnist.train.labels [N 10]
mnist = input_data.read_data_sets(data_dir, one_hot=True)
return mnist
Import the TensorFlow, and datatool functions (ensure Python can read the functions from other directories by creating a file named __init__.py in those directories):
import tensorflow as tf
from datatool.datasets import read_tf_mnist
Loading MNIST by using our datatool:
mnist = read_tf_mnist("MNIST_data")
Define model: creating placeholders to assign data at on. For our classification problem on MNIST, the data consists of raw images and their labels. Therefore, we need declare two placeholders:
x = tf.placeholder(tf.float32,[None,784])
y_ = tf.placeholder(tf.float32,[None,10])
x stores the image data ((which was vectorized in MNIST)) in type float tf.float32. [None,784] indicates data dimension of 784 with no constraint of image number can be put in the placeholder. Similarly for _y as the ground-truth label of 10 dimension.
Declare variables W for weights and b for bias to model the regression problem: y = f(W*x+b), f is the softmax function.
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
For similarity, we initialize W and b with zero matrices by tf.zeros which works with linear model. However, the zero weights are not applicable for deep neural network in the next examples. We then can define the model and define loss function of cross entropy:
y = tf.nn.softmax(tf.matmul(x, W) + b)
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y),reduction_indices=[1]))
tf.nn.softmax to compute softmax function. Because _y and y are matrices of [None,10]. y_ * tf.log(y) is the element-wise multiplication, and tf.reduce_sum(y_ * tf.log(y),reduction_indices=[1]) computes sum of elements of each row. To understand more about the function tf.reduce_sum, let’s take a look this example:
# 'x' is [[1, 1, 1]
# [1, 1, 1]]
tf.reduce_sum(x) ==> 6
tf.reduce_sum(x, 0) ==> [2, 2, 2]
tf.reduce_sum(x, 1) ==> [3, 3]
tf.reduce_sum(x, 1, keep_dims=True) ==> [[3], [3]]
tf.reduce_sum(x, [0, 1]) ==> 6
ON another way, TF supports the softmax by simple function, which operates more efficient tf.nn.softmax_cross_entropy_with_logits. It is recommended to use instead of tf.nn.softmax because it covers numerically unstable corner cases in the mathematically right way.
y = tf.matmul(x, W) + b
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
Choose the optimizer for training by using Gradient Descent with learning rate 0.5:
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
To encapsulate the environment in which Operation objects are executed and and Tensor objects are evaluated, we need a Session:
with tf.Session() as sess:
# init the variables
sess.run(tf.global_variables_initializer())
# training with 1000 iterations
for _ in range(1000):
# 100 sample per batch
batch_xs, batch_ys = mnist.train.next_batch(100)
# run training
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
# evaluation
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
The model is fined above has no value until starting the session. tf.global_variables_initializer() initialize all parameters of the model. Then, the training is performed through 1000 iterations:
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
Each batch has 100 samples, and you need to specify the value of the learning phase as part of feed_dict corresponding with placeholder you defined at the beginning. Similarly for evaluation but conducted on test set of MNIST.
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
The complete code is here tf_mnist_softmax.py:
#!/usr/bin/python
import tensorflow as tf
from datatool.datasets import read_tf_mnist
mnist = read_tf_mnist("MNIST_data")
x = tf.placeholder(tf.float32,[None,784])
y_ = tf.placeholder(tf.float32,[None,10])
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
y = tf.matmul(x, W) + b
# The loss function by cross entropy
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
# Test trained model
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
with tf.Session() as sess:
# init the variables
sess.run(tf.global_variables_initializer())
# training with 1000 iterations
for _ in range(1000):
# 100 sample per batch
batch_xs, batch_ys = mnist.train.next_batch(100)
# run training
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
# evaluation
print("Accuracy: ", sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
Run TF program:
>> python tf_mnist_softmax.py
>> ('Accuracy: ', 0.91909999)
The accuracy is about 92%, which is not good on MNIST, because we used only one fully-connected layer. We’ll try to improve the accuracy in next examples.
Keras
In this session, we try to simplify TF by Keras, and minimize the change to keep the transition smooth:
Model definition from TF:
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x, W) + b)
To Keras which provide the layer Dense (fully-connected layer) can operate in similar, but shorter way:
from keras.layers import Dense
y = Dense(10, activation='softmax')(x)
The loss function defined above of TF:
# The loss function by cross entropy
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
# Test trained model
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
can be replaced by a built-in function of Keras:
from keras.objectives import categorical_crossentropy
from keras.metrics import categorical_accuracy as accuracy_eval
cross_entropy = tf.reduce_mean(categorical_crossentropy(y_, y))
# Test trained model
correct_prediction = accuracy_eval(y_, y)
The complete code with Keras is here keras_mnist_softmax.py:
#!/usr/bin/python
import tensorflow as tf
from datatool.datasets import read_tf_mnist
import keras
from keras.layers import Dense
from keras.objectives import categorical_crossentropy
from keras.metrics import categorical_accuracy as accuracy_eval
mnist = read_tf_mnist("MNIST_data")
x = tf.placeholder(tf.float32,[None,784])
y_ = tf.placeholder(tf.float32,[None,10])
y = Dense(10, activation='softmax')(x) # fully-connected layer of output layer of 10 units with a softmax activation
cross_entropy = tf.reduce_mean(categorical_crossentropy(y_, y))
# Test trained model
correct_prediction = accuracy_eval(y_, y)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
with tf.Session() as sess:
# init the variables
sess.run(tf.global_variables_initializer())
# training with 1000 iterations
for _ in range(1000):
# 100 sample per batch
batch_xs, batch_ys = mnist.train.next_batch(100)
# run training
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
# evaluation
print("Accuracy: ", sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
Run new program and obtain the similar accuracy as above:
>> python keras_mnist_softmax.py
>> ('Accuracy: ', 0.91790003)
However, in this case we use Keras only as shortcut to map inputs to outputs, and built-in functions provided in Keras. The optimization is done via native TF optimizer rather than Keras optimizer. We do not even use Keras Model at all.
Example 2: MNIST classification by LeNet
In this tutorial, we will improve the accuracy by using LeNet, a first architecturee of CNN first introduced by Lecun et al, 1998 in their paper: Gradient-Based Learning Applied to Document Recognition. We learn how to implement this network architecture in native TF, and by using Model of Keras. But, let’s start with the basic understanding of LeNet.
LeNet is the first CNN designed primarily for OCR and character recognition in documents. It is straightforward and pretty small, making it perfect for learning basics of CNN. It can even run on CPU, which is good if your system doesn’t support GPU. The architecture of LeNet consists of following layers: Two convolution layers (each layer followed by ReLU (Rectified Linear Unit) + Pooling), one Fully-Connected (FC) layer + ReLU, and the last FC:
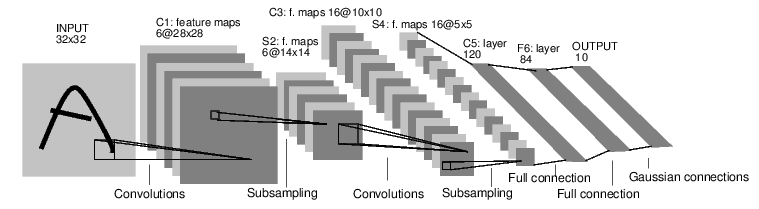
The input and output size of layers of LeNet5 are described as follows.
INPUT(32x32)
--> CONV(Filter size: 5x5x6 -> Ouput: 28x28x6)
--> RELU(Ouput: 28x28x6)
--> POOL(Ouput: 14x14x6)
--> CONV(Filter size: 5x5x16, Ouput: 10x10x16)
--> RELU(Ouput: 10x10x16)
--> POOL(Ouput: 5x5x16)
--> FLATTEN(Ouput: 400)
--> FC(Ouput: 120)
--> RELU => FC(Ouput: 10)
Note that the image size accepted by LeNet is 32x32. Four types of layers build LeNet5: Convolution, ReLU, Pooling and FC, in which ReLU and Pooling does not need parameters. Using native TF have to repeat the same code line many times. Therefore, before implementing LeNet5 architecture in TF, we define some wrapper functions of TF to facilitate the process:
To declare variables (weight and bias), we similarly use tf.Variable function, but weight is initialized ramdomly and bias is intialized as constant:
# initialize weights/filters
def init_weight(shape):
weight = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(weight)
# initialize bias
def init_bias(shape):
bias = tf.constant(0.1, shape=shape)
return tf.Variable(bias)
For convolution layer, beside conv_2d, we define conv_2d_1x1_valid to shorten the code as this convolution parameters are used many times:
# convolution layers
def conv_2d(w,W,strides=[1, 1, 1, 1],padding="SAME"):
return tf.nn.conv2d(x,W,strides,padding)
def conv_2d_1x1_valid(x,W):
return tf.nn.conv2d(x,W,strides=[1, 1, 1, 1],padding="VALID")
Activation layer:
# relu
def relu(x):
return tf.nn.relu(x)
Similar to convolutioin, we delare shorter function for pooling layer:
# max pooling layers
def pool_max(x,ksize,strides,padding):
return tf.nn.max_pool(x, ksize, strides, padding)
def pool_max_2x2_2x2_valid(x):
return tf.nn.max_pool(x,ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1],padding="VALID")
Flatten and fully connected layers:
# flatten
def flatten(x):
return tf.contrib.layers.flatten(x)
# Fully connected layers
def dense_fc(x,W,b):
return tf.matmul(x,W) + b
All above functions are declared in, eg. layers/cnn_layers.py:
import tensorflow as tf
# initialize weights/filters
def init_weight(shape):
weight = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(weight)
# initialize bias
def init_bias(shape):
bias = tf.constant(0.1, shape=shape)
return tf.Variable(bias)
# convolution layers
def conv_2d_1x1_valid(x,W):
return tf.nn.conv2d(x,W,strides=[1, 1, 1, 1],padding="VALID")
def conv_2d(w,W,strides=[1, 1, 1, 1],padding="SAME"):
return tf.nn.conv2d(x,W,strides,padding)
# relu
def relu(x):
return tf.nn.relu(x)
# max pooling layers
def pool_max(x,ksize,strides,padding):
return tf.nn.max_pool(x, ksize, strides, padding)
def pool_max_2x2_2x2_valid(x):
return tf.nn.max_pool(x,ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1],padding="VALID")
# flatten
def flatten(x):
return tf.contrib.layers.flatten(x)
# Fully connected layers
def dense_fc(x,W,b):
return tf.matmul(x,W) + b
and, LeNet5 in TF can be implemented more concise:
from layers import cnn_layers as cnn
def lenet5(x_image):
# Layer 1: Conv-ReLU-Pool
W_conv1 = cnn.init_weight([5,5,1,6])
b_conv1 = cnn.init_bias([6])
h_conv1 = cnn.relu(cnn.conv_2d_1x1_valid(x_image,W_conv1) + b_conv1)
h_pool1 = cnn.pool_max_2x2_2x2_valid(h_conv1)
# Layer 1: Conv-ReLU-Pool
W_conv2 = cnn.init_weight([5,5,6,16])
b_conv2 = cnn.init_bias([16])
h_conv2 = cnn.relu(cnn.conv_2d_1x1_valid(h_pool1,W_conv2) + b_conv2)
h_pool2 = cnn.pool_max_2x2_2x2_valid(h_conv2)
# Flatten (5x5x16) = 400
h_pool2_flatten = cnn.flatten(h_pool2)
# Dense fully connected layers 1
W_fc1 = cnn.init_weight([400,120])
b_fc1 = cnn.init_weight([120])
h_fc1 = cnn.relu(cnn.dense_fc(h_pool2_flatten,W_fc1,b_fc1))
# Dense fully connected layers 2
W_fc2 = cnn.init_weight([120,84])
b_fc2 = cnn.init_weight([84])
h_fc2 = cnn.relu(cnn.dense_fc(h_fc1,W_fc2,b_fc2))
# Dense fully connected layers 3
W_fc3 = cnn.init_weight([84,10])
b_fc3 = cnn.init_weight([10])
logits = cnn.dense_fc(h_fc2,W_fc3,b_fc3)
return logits
We re-use the training and testing code as in example 1 except some following changes:
(1) Add pad to obtain 32x32 size from 28x28 size of MNIST (eg. in datatool/datasets.py)
def resize_mnist_32x32(data):
if data.shape[1] == 784:
data = tf.reshape(data,[-1,28,28,1])
data = np.pad(data, ((0,0),(2,2),(2,2),(0,0)), 'constant')
elif data.shape[1] == 28 and data.shape[2] == 28:
data = np.pad(data, ((0,0),(2,2),(2,2),(0,0)), 'constant')
else:
print "MNIST format is not supported."
return data
(2) Training with Adam optimization algorithm with smaller learning rate:
learning_rate = 0.001
train_step = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)
(3) We implement to store checkpoint after training:
saver = tf.train.Saver() #to declare saver for checkpoint
...
saver.save(sess,'lenet5') #to save session
...
saver.restore(sess,tf.train.latest_checkpoint('.')) #restore the session
The complete TF for LeNet5 as below (eg. tf_mnist_lenet.py):
#!/usr/bin/python
import tensorflow as tf
from datatool.datasets import read_tf_mnist, resize_mnist_32x32
from layers import cnn_layers as cnn
# LeNet 5 architecture
# INPUT(32x32)
# => CONV(F: 5x5x6 -> O: 28x28x6)
# => RELU(28x28x6)
# => POOL(14x14x6)
# => CONV(F: 5x5x16, O: 10x10x16)
# => RELU(10x10x16)
# => POOL(5x5x16)
# => FLATTEN(400)
# => FC(120)
# => RELU => FC(10)
def lenet5(x_image):
# Layer 1: Conv-ReLU-Pool
W_conv1 = cnn.init_weight([5,5,1,6])
b_conv1 = cnn.init_bias([6])
h_conv1 = cnn.relu(cnn.conv_2d_1x1_valid(x_image,W_conv1) + b_conv1)
h_pool1 = cnn.pool_max_2x2_2x2_valid(h_conv1)
# Layer 1: Conv-ReLU-Pool
W_conv2 = cnn.init_weight([5,5,6,16])
b_conv2 = cnn.init_bias([16])
h_conv2 = cnn.relu(cnn.conv_2d_1x1_valid(h_pool1,W_conv2) + b_conv2)
h_pool2 = cnn.pool_max_2x2_2x2_valid(h_conv2)
# Flatten (5x5x16) = 400
h_pool2_flatten = cnn.flatten(h_pool2)
# Dense fully connected layers 1
W_fc1 = cnn.init_weight([400,120])
b_fc1 = cnn.init_weight([120])
h_fc1 = cnn.relu(cnn.dense_fc(h_pool2_flatten,W_fc1,b_fc1))
# Dense fully connected layers 2
W_fc2 = cnn.init_weight([120,84])
b_fc2 = cnn.init_weight([84])
h_fc2 = cnn.relu(cnn.dense_fc(h_fc1,W_fc2,b_fc2))
# Dense fully connected layers 3
W_fc3 = cnn.init_weight([84,10])
b_fc3 = cnn.init_weight([10])
logits = cnn.dense_fc(h_fc2,W_fc3,b_fc3)
return logits
mnist = read_tf_mnist("MNIST_data")
x = tf.placeholder(tf.float32,[None,32,32,1])
y_ = tf.placeholder(tf.float32,[None,10])
# lenet5
y = lenet5(x)
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
# Test trained model
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# learning parameters
learning_rate = 0.001
num_iteration = 20000
batch_size = 100
#train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
train_step = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)
saver = tf.train.Saver()
# training
with tf.Session() as sess:
# init the variables
sess.run(tf.global_variables_initializer())
# training with 1000 iterations
for i in range(num_iteration):
# 100 sample per batch
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# run training
sess.run(train_step, feed_dict={x: resize_mnist_32x32(batch_xs), y_: batch_ys})
if i % 50 == 0:
print("Iteration: ", i)
print("Evaluation accuracy: ", sess.run(accuracy, feed_dict={x: resize_mnist_32x32(mnist.validation.images), y_: mnist.validation.labels}))
saver.save(sess,'lenet5')
# test
with tf.Session() as sess:
saver.restore(sess,tf.train.latest_checkpoint('.'))
print("Test accuracy: ", sess.run(accuracy, feed_dict={x: resize_mnist_32x32(mnist.test.images), y_: mnist.test.labels}))
The accuracy of LeNet5 on MNIST is much better than logistic regression:
>> python tf_mnist_lenet.py
>> ('Test accuracy: ', 0.99040002)
Refer to here to know current state of the art on MNIST dataset.
To be continued
